BLS Deep Dive | SKALE

If you're in the blockchain or cryptography communities, you've likely heard of BLS signatures. Over the past few months, we've been working on our own open source implementation and will be reviewing the technology as well as our implementation of it at SKALE.
Multi-signature Verification
Traditional multi-signature verification is slow and cumbersome — it requires multiple communication rounds to ensure that m of n participants have signed. And in the case of consensus protocols, such schemes require all signatures to be stored across the entire network. But, thanks to BLS, we can replace the need to store all of these separate signatures with one aggregate signature which is comprised of some threshold of these signatures!
Aside from storage efficiencies, this allows for improvements insofar as network bandwidth as a result of the reduced communication between nodes as well as a decrease in computation for having to verify signatures. And it is these efficiencies which have helped to contribute to the 20k TPS that SKALE has managed to achieve in its early SKALE Chain implementations.
The first step in this our implementation is known as Distributed Key Generation (DKG) where we securely generate keys for each of n participants, where any threshold t + 1 of n participants could sign a message for a whole group.
Distributed Key Generation (DKG)
At SKALE, we use a modified version of the Joint-Feldman Protocol which uses sets of points on elliptic curves supported by Ethereum. To start, we have two sets of points on the elliptic curves:
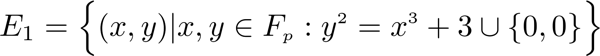
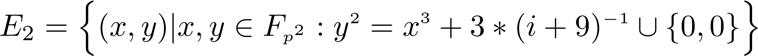
Note: It should be noted that secret keys are from the Fp group while public key(s) are from G₂. Signature and message hashes are from the G₁ group, where G₁ is an additive subgroup of E₁ generated by point P₁ and G₂ is an additive subgroup of E₂ generated by point P₂. It is known that G₁ and G₂ are the only cyclic groups of order q on E₁ and E₂ respectively (with well-chosen P₁ and P₂). p and q are 256-bit prime numbers.
And leveraging these two sets of points, SKALE's DKG on the Ethereum Mainner performs the following:

After each node knows its own secret key and the group’s public verification value has been stored in the SKALE DKG smart contract, node(s) can create verifiable BLS signatures.
Boneh-Lynn-Shacham (BLS)
Before moving into implementation, we must first understand the following information problems:
Computational Diffie-Hellman
In a cyclic group, if you know: (g, g * x, g * y), determine g * xy.
Decisional Diffie-Hellman
In a cyclic group, if you know (g, g * x, g * y, g * z), determine if z ≟ xy
Co-decisional Diffie-Hellman
In two cyclic groups, if you know (a, a * x, b, b * y) where a ∈ G₁ and b ∈ G₂, determine if x ≟ y.
BLS uses a ‘pairing’ to make the Computation and Decisional problems hard in both of our groups, but the Co-decisional problem easy. This is done with a magical function known as a ‘Bilinear Mapping’.
Bilinear Mapping
A bilinear mapping is an very unique function in that it moving around exponents within it or multiplying doesn’t matter / change its result. At SKALE, we use a bilinear mapping for additive (in lieu of multiplicative) abstract groups with the property that multiplying does not change the result.
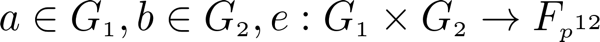
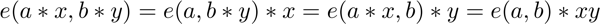
Note: SKALE uses this implementation based on this scheme.
Signature Scheme
This bilinear mapping allows us to create a signature scheme where we multiply the secret key by the hash of the message to create our signature. This scheme is represented below:
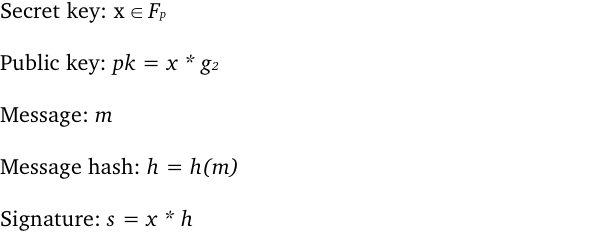
With this scheme, verification is simple and only requires checking if the pairing of the signature and our generator point in E₂ is equal to the pairing of message hash and the public key.
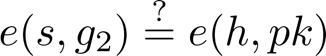
Aggregate Signatures

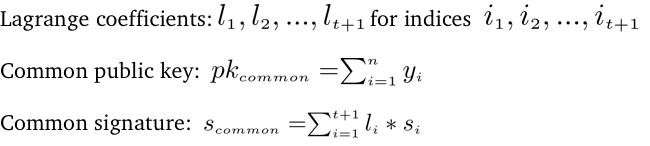
For verification, we check if the pairing of the sum of the aggregated signatures multiplied by their corresponding Lagrange coefficients and our generator point on E₂ is equal to the pairing of message hash and the common public key.
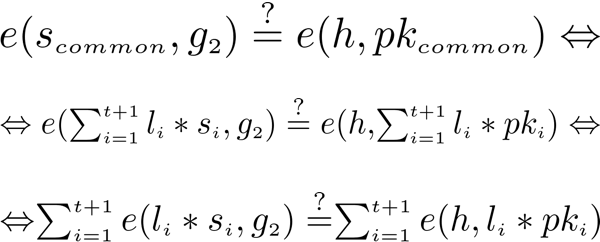
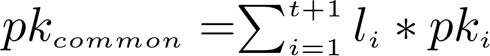
Learn More
With DKG and BLS, SKALE has managed to exceed over 20k transactions and achieve finality in its SKALE Chains. If you'd like to check out our BLS library, you can see the code here.
And if you are interested in learning more about DKG, check out the Wikipedia page as well as the academic paper (viewable by purchase only). Additional information on Ethereum cryptography can also be found in the Yellowpaper at Appendix E. Precompiled Contracts.
SKALE’s mission is to make it quick and easy to set up a cost-effective, high-performance SKALE Chain that runs full-state smart contracts. We aim to deliver a performant experience to developers that offer speed and functionality without giving up security or decentralization. Follow us here on Telegram, Twitter, and Discord, and sign up for updates via this form on the SKALE website.
.webp)
.webp)
.webp)





